BetaZero: Tabula Rasa Tic-Tac-Toe¶
November 17 2018
tldr: I describe experiments with a reinforcement learning algorithm that trains an agent to play tic-tac-toe tabula rasa. The agent queries a neural network (NN) that values board configurations. The weights of the network are optimized by an evolution strategy (CMA-ES). The agent learns by playing against a novel adversary that values board configurations by simulating random play against the NN agent.
Source available on github.
Intro¶
In 2017 two widely-read AI papers were published, one by Google's DeepMind -- Mastering the game of Go without Human Knowledge [ https://www.nature.com/articles/nature24270, https://deepmind.com/documents/119/agz_unformatted_nature.pdf ] -- and one by OpenAI -- Evolution Strategies as a Scalable Alternative to Reinforcement Learning [ https://arxiv.org/abs/1703.03864 ]. The former describes AlphaZero, a deep reinforcement learning algorithm that learned Go just by playing games against itself. The latter makes the point that evolution strategies can have some advantages over RL methods, particularly in problems which have delayed and sparse rewards, like the game of Go.
To get a better understanding of these papers, let's train an agent to play a game using an evolution strategy.
Playing Go seems to take a larger amount of computational resources than I have access to (ex., DeepMind used over 5000 TPUs [ https://en.wikipedia.org/wiki/AlphaZero ]), and it's always a good idea to start simple, so let's play tic-tac-toe instead. It's similar to Go in that it's zero-sum (one player's win is the other's loss), and provides perfect information. (The board is visible to both players, and there are no hidden elements.) Additionally, there is no randomness like dice or a spinner. The difference is that in tic-tac-toe there are vastly fewer possible board configurations (roughly 5812 according to [ http://brianshourd.com/posts/2012-11-06-tilt-number-of-tic-tac-toe-boards.html ]) than in Go ($\sim 2 * 10^{170}$ [https://en.wikipedia.org/wiki/Go_and_mathematics#Legal_positions ] ).
In the interest of simplicity, let's make the agent a neural network. AlphaZero's agent was more complex (see below).
Finally, let's add some more constraints to better define the problem: First, the agent must learn tabula rasa -- purely from self play (ex., no hints about or examples of good moves). Second, the agent must play perfectly (be unbeatable). Third, the learning must be stable, in the sense that once the agent achieves perfect play, it should continue to play perfectly.
AI for Game Play¶
An algorithm for perfect play in zero-sum, perfect information games like tic-tac-toe, chess, and Go is known. It is the minimax algorithm [ https://en.wikipedia.org/wiki/Minimax, https://pdfs.semanticscholar.org/64a0/3e75e867b67de855d6d6c6013df9600d53ae.pdf ]. The idea is to imagine the current game board as the root node of a tree, with each child node representing the board after you take a turn (a turn is called a ply; a move is when each player takes a turn, i.e., two plies). Each of their children represents the board after the other player takes a turn, and so on, until the game ends. The leaves of the tree are the boards of games that have ended. Note that each edge connecting a parent node to a child node represents a ply. In any path from root to leaf, the edges alternate between representing your move and representing your opponents because these are turn-taking games.
Each node (board configuration) can be assigned a value: A leaf is assigned +1 if you win, -1 if you lose, and 0 if you draw. Other nodes in the tree (evaluated from the bottom up), are given a value by asking: Which of my child nodes has the best value for the player whose turn is represented by the edge between us? You are trying to maximize the value of your moves knowing (or assuming) that your opponent will choose to do the same. Alternatively, you maximize the value of your moves knowing that your opponent will choose to minimize your valuation of his moves.
If this algorithm, minimax, solves zero-sum, perfect information games, why is there an AlphaZero? The reason is that computing the entire game tree is impossible for complex games like chess or Go. The tree is simply too large to compute or store. Approximate algorithms (alpha-beta pruning, Monte Carlo Tree Search (MCTS) ), canned moves ("opening books"), and heuristics make computing the game tree more efficient, and if you've ever played chess against a computer you've likely been playing against move-selection methods like these.
Monte Carlo Tree Search¶
MCTS [ http://ccg.doc.gold.ac.uk/wp-content/uploads/2016/10/browne_tciaig12_1.pdf ] is the state-of-the-art approximate algorithm. Starting with just a root node, MCTS builds a partial game tree and estimates the value of its nodes by iterating the following:
- Selection: Descend the tree from the root, choosing which child to visit next based on a policy that balances the desire to build a tree of high-value nodes with the desire to reduce the error in the estimate of the value of the node. (To learn about this decision mechanism, upper-confidence bound 1 applied to trees, UCT, see [ http://ggp.stanford.edu/readings/uct.pdf ].)
- Expansion: Add a child node, if possible, to the selected leaf node.
- Simulation: Simulate game play from the new child node until the end of the game choosing moves randomly for both players (a monte carlo game simulation). Use the result of that game (r = +1, -1 or 0) as the value estimate of this new node like so: $sum_{node} = r, n_{node} = 1$
- Backpropagation: Refine the estimate of all of this node's ancestor nodes like so: $sum_{ancestorNode} += r, n_{ancestorNode} += 1$ -- but flip the sign of r if the node's "child edges" represent the opponent's turn, just like in minimax.
In all cases, the value of a node is estimated as $E[v] = sum/n$
This loop may be run until a computational budget is exhausted. It has been shown that MCTS+UCT converges to minimax as the computation budget increases to infinity [ http://www.ics.uci.edu/~dechter/courses/ics-295/winter-2018/papers/mcts-gelly-silver.pdf ].
AlphaZero¶
AlphaZero's game-playing agent takes MCTS and replaces the monte-carlo estimate of the node's value (in step (3), above) with a neural network's (NN's) estimate. The NN's input is a board configuration (a node). (Along with a value estimate, the NN also outputs the probability of selecting a move (of each child edge). This probability is used by UCT in step 1. See [ https://deepmind.com/documents/119/agz_unformatted_nature.pdf ] for more details.)
To train the agent, the researchers repeated these two steps: First have the agent play many games against itself, collecting the board configurations (state) and the game outcomes (return) along the way. Next, use these (state, return) pairs to train the network via supervised learning (backpropagation and SGD) to predict return from state.
Note that no information about the game (Go, chess, or shogi) was provided to the agent. It learned tabula rasa.
So how did they know whether the agent was improving if it was only playing against itself? They benchmarked the agent's performance against existing game-play agents (including previous versions of "Alpha" algorithms -- AlphaLee and AlphaGo -- and against human beings). These benchmark results were not fed back into the learning process, however. The agent only learned from the results of self play.
Evolution Strategies¶
Evolution strategies (ES's) are algorithms for black-box optimization over real-valued vector parameters that maintain a set of K parameters (sometimes called a population) at each iteration (or "generation"). Each (vector) parameter in the set is evaluted and assigned an objective value (a "fitness"). The ES uses all of the K parameters and fitness values to determine the population for the next generation.
OpenAI's paper, Evolution Strategies as a Scalable Alternative to Reinforcement Learning, decribes computational experiments with an ES that estimates the gradient of the fitness using the current population and takes a step in that direction (to increase the fitness). They ran the algorithm on many OpenAI gym [ https://gym.openai.com ] environments and compared the results to RL algorithms.
They observed:
- ES algorithms work relatively well on problems with sparse and long-term rewards. In a general RL problem, an agent may receive a reward for every action it takes and use these rewards to improve its choice of action. ES's ignore these single-step rewards and look only at the final, long-term return (sum of all single-step rewards) of a task. The RL algorithms tested had some difficulty on tasks where most of the rewards were zero (very little immediate feedback), or where an action might induce a reward many steps later. Games like tic-tac-toe supply rewards only at the end, and all moves (even early ones) influce the outcome. In these aspects, ES algorithms seem ideally suited to optimizing a game-playing agent.
- The ES algorithm chosen had few hyperparameters and seemed to be robust to the choice of their values. The researchers were able to use the same hyperparameters for all tasks they experimented with.
- Evolution strategies are highly paralleliizable. Fitness evaluations are independent, so they may all be run simultaneously on different CPUs without communication during the run.
Observation 1 suggests ES's are worth trying on this kind of task. Observation 2 reduces the time I have to spend fiddling with hyperparameters. Observation 3 make an ES a good fit for the computer to which I happen to have access: one with many cores and no GPU.
Not long after OpenAI's paper, Uber AI released five papers giving detailed comparisons of evolution algorithms (EA's, of which evolution strategies are a subset) to traditional RL methods [ https://eng.uber.com/deep-neuroevolution/ ]. The EA's were found to be competitive with the RL methods.
Self-play¶
Self-play is bit mysterious to me. That's mainly what motivated me to pursue this project. How can an agent learn anything without a fixed objective? What would it optimize, exactly?
Self-play has a long history. In 1959 Arthur Samuel [ https://www.semanticscholar.org/paper/Some-Studies-in-Machine-Learning-Using-the-Game-of-Samuel/26337762b9b06c7d8a952bebab6408a5e7f9935d ] wrote a program that learned to play checkers using various methods, including self-play. In 1992, Gerald Tesauro [ http://papers.nips.cc/paper/465-practical-issues-in-temporal-difference-learning.pdf ] created TD-Gammon, a neural network trained to play backgammon at a world-champion level. This NN learned solely by self-play using a method similar to that described above for AlphaZero -- without MCTS. TD-Gammon's NN value estimates were used directly to choose moves. In 2016-2017, AlphaZero learned by self-play to play Go, chess, and shogi as world-class levels. Recently, OpenAI trained a neural network to play a video game called Dota 2 [ https://openai.com/five/ ] via self-play.
Self-play is fraught with potential problems:
- An agent that plays itself could learn a cooperative behavior. For example, I was able to train a tic-tac-toe agent by pure self play (each agent -- defined by its parameter value -- was played only against itself) to never lose, but it learned only to play a single game where it would always draw. It always lost to a minimax player.
- An agent could "invent" many strategies and learn to play against them but simply never be exposed to other strategies and, thus, lose if an external agent played them.
- What if there exists a strategy A that beats strategy B that beats strategy C that -- in turn -- beats strategy A? Think of "A, B, and C" as "rock, paper, and scissors". One could imagine the learning process getting caught in a loop and then being vulnerable to any of A, B, or C, depending on when learning is halted. OpenAI reports something they call "strategy collapse" [ https://blog.openai.com/openai-five/ ], which sounds like this. The potential for cycles of strategy dominance in backgammaon self-play was reported in [ http://www.demo.cs.brandeis.edu/papers/alife5.pdf ].
Some ways to mitigate these problems are:
- Don't engage in exact self-play. Instead, choose the last, best parameter value, instantiate an agent with that parameter, and use it as the opponent in the fitness evaluation of new parameters. (Used in AlphaGo.)
- Use more than one previous "champion" in the fitness evaluation. The set of previous champions is sometimes called a "hall of fame" [ https://pdfs.semanticscholar.org/148e/2d94529956d13d987309e04cf771828fb7a0.pdf ]. (Used in Dota2 to avoid strategy collapse.)
- Use search (ex., MCTS) to find better moves than the current agent could find on its own. Injecting this extra information into the training might help break cycles and explore the game space. (Used in AlphaGo)
- Include randomness to promote exploration of the game-board space. (Used in AlphaGo and Dota2. Appears in TD-Gamma via dice rolls in normal game play.)
Self-play's cousin in the evolution algorithm literature is coevolution [ https://arxiv.org/pdf/1506.05082.pdf ]. This paper [ http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=F85E8E6AA1887B769186418950106F1F?doi=10.1.1.51.6373&rep=rep1&type=pdf ] compares RL self-play to coevolution.
BetaZero¶
Our agent (see nnPlayer.py) has at its core a neural network (NN) that takes a board configuration as input and produces a (scalar) value estimate as output. For any given board configuration the agent queries the NN with the board configurations that would be produced by each legal move. (You might consider this a "one-ply" search.)
The NN takes 18 inputs: 9 of them for X and 9 for O. Each input represents one space on the 3x3 tic-tac-toe grid. It contains a 1 if the space is occupied and 0 otherwise. The NN has two hidden layers, each with 18 nodes. This gives a total of 703 parameters.
Each node has biases and uses a tanh activation function.
The agent is deterministic except if there's a tie -- when more than one move yields the same value. A tie is broken randomly. (Two value estimates are considered "equal" if they are within $\varepsilon = 10^{-6}$ of each other.)
Fitness¶
To evalute a parameter, the agent plays against an Omniscient Adversary (OA). To select a move, OA simulates games for each legal move and averages the returns. In the simulation OA chooses its own moves randomly but uses an "embedded" agent to choose its opponent moves. The embedded agent, ideally, is the opponent itself. In other words, the OA knows what moves its opponent would make for each board state and can use that information to beat its opponent.
The OA is easy to program. It only uses forward passes. There is no tree to build and no backpropagation (in the MCTS sense) to run.
Also, it can beat a minimax player. This is not the case, for example, for a pure monte carlo game simulation. Playing a pure monte carlo player against a minimax player 100 times using $nPlay$ simulations to evaulate each move yields:
nPlay = 1 W = 0.000 D = 18.500 L = 81.500 n = 100.000 nPlay = 10 W = 0.000 D = 52.500 L = 47.500 n = 100.000 nPlay = 100 W = 0.000 D = 75.500 L = 24.500 n = 100.000 nPlay = 1000 W = 0.000 D = 79.000 L = 21.000 n = 100.000 nPlay = 10000 W = 0.000 D = 82.500 L = 17.500 n = 100.000
where W,D,L count the number of wins, losses, or draws in n = 100 games.
The monte carlo (MC) player (see mcPlayer.py) still loses against the minimax (MM) player (see mmPlayer.py) even when using 10,000 simulations to evaluate each move. This is because the MC player considers it just as likely that its opponent will choose a winning move as any other legal move. Contrast this to minimax or MCTS which assume their opponents will maximize their own chances of winning.
In contrast, if we embed the minimax player in OA instead of the neural network then, with $nPlay=100$ simulations to evaluate each move, OA never loses to MM:
nPlay = 1 W = 0.000 D = 49.500 L = 50.500 n = 100.000 nPlay = 3 W = 0.000 D = 70.500 L = 29.500 n = 100.000 nPlay = 10 W = 0.000 D = 91.500 L = 8.500 n = 100.000 nPlay = 30 W = 0.000 D = 98.500 L = 1.500 n = 100.000 nPlay = 100 W = 0.000 D = 100.000 L = 0.000 n = 100.000
Why not train against MCTS? MCTS (see mctsPlayer.py) is proven to converge to minimax, but seems to take more simulations to achieve the same quality as OA. (Note that $nBudg$ is the simulation budget for evaluating all legal moves, whereas $nPlay$ is the budget for evaluating a single legal move.):
nBudg = 1 W = 0.000 D = 11.500 L = 88.500 n = 100.000 nBudg = 3 W = 0.000 D = 22.500 L = 77.500 n = 100.000 nBudg = 10 W = 0.000 D = 37.000 L = 63.000 n = 100.000 nBudg = 30 W = 0.000 D = 48.000 L = 52.000 n = 100.000 nBudg = 100 W = 0.000 D = 72.500 L = 27.500 n = 100.000 nBudg = 300 W = 0.000 D = 88.000 L = 12.000 n = 100.000 nBudg = 1000 W = 0.000 D = 95.500 L = 4.500 n = 100.000 nBudg = 3000 W = 0.000 D = 97.000 L = 3.000 n = 100.000 nBudg = 10000 W = 0.000 D = 98.000 L = 2.000 n = 100.000
Additionally, OA is much simpler to program. While OA can't be used for game play directly -- since an actualy opponent wouldn't tell you her moves -- it can be used for training an agent.
Why not just train against MM? While we can compute minimax completely for tic-tac-toe, that wouldn't work for more complex games like chess or go.
Optimization¶
Covariance Matrix Adaptation ES (CMA-ES [ https://arxiv.org/abs/1604.00772 ]) is a state-of-the-art ES algorithm with an easy-to-use Python package, so we'll use that.
A fitness evaluation is the number of losses in 100 games against OA.
OA requires random numbers choose its moves in its simulations. Both OA and NN break ties in their evaluation functions randomly. This randomness in the fitness function can impede progress of the optimizer (see results below). To make the fitness deterministic -- and improve the efficiency of the optimization -- the random number generators are seeded. At the outset of the optimization 100 seeds are chosen (randomly). These seeds are saved and used to seed each of the 100 corresponding games played against OA every time the fitness is evaluated.
OA embeds not the agent defined by the parameter being evaluated, but that of a fixed "best-so-far" parameter. When a new parameter is found that loses fewer than 10 times out of 100 games to OA, it becomes the new, fixed, "best-so-far" parameter.
Each generation requires 23 parameters X 100 games/parameter = 2300 games. These evaluations are parallelized across multiple cores using Python's multiprocessing package (see evaluator.py, pool.py).
External Benchmark¶
To know whether the optimization is producing agents that can play tic-tac-toe well we periodically take the best agent and have it play 100 games against MM (N.B. mmPlayer.py uses the minimax implementation from Dwayne Crooks's Python package xo).
Results¶
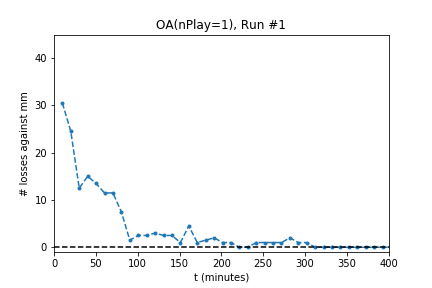
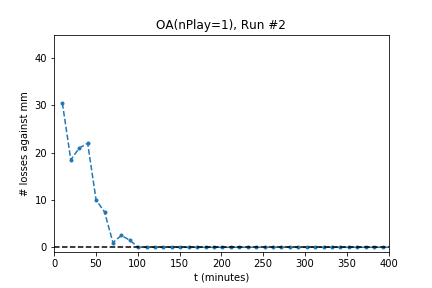
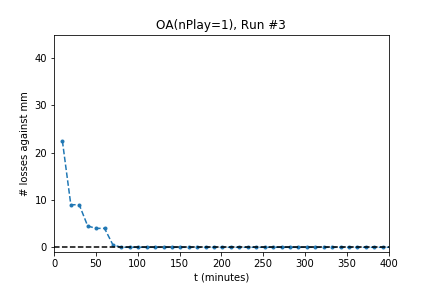
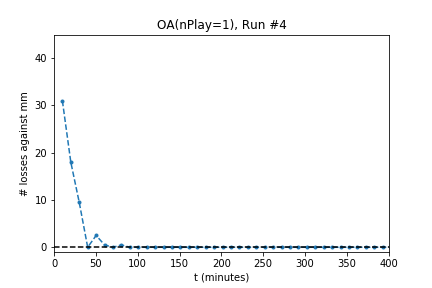
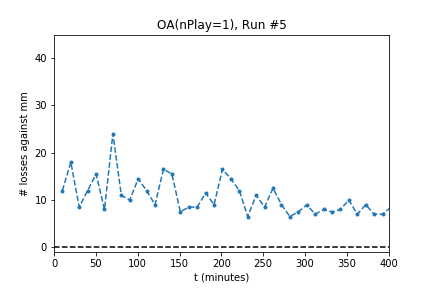
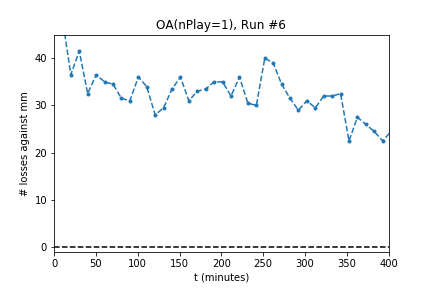
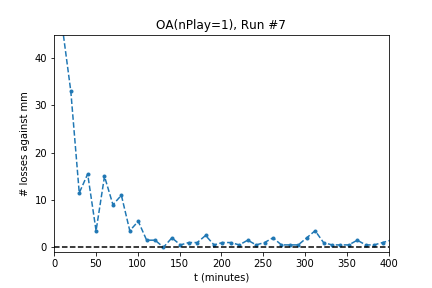
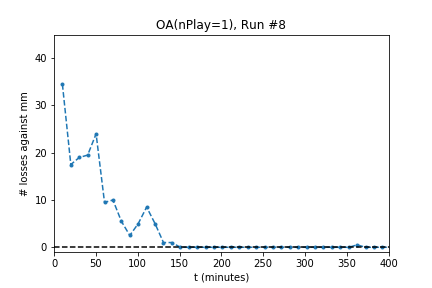
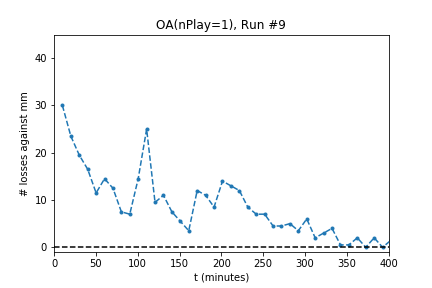
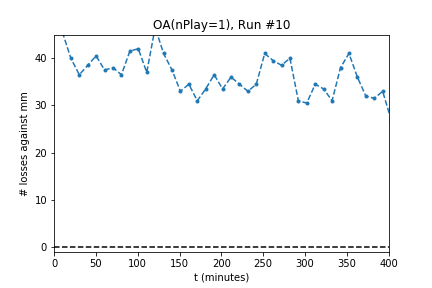
In five out of ten runs the agent achieves perfect play -- 0 losses in 100 games against the minimax player. Additionally, the process is stable: As the optimization continues the agent continues to achieve (or revert to) zero losses.
The optimization produces a perfect player only half of the time. Using the external evaluation (playing against MM) is it easy to tell which player is best. However, the goal is to produce a player using only self-play information. To do so, use the following process:
- Run N independent optimizations starting at N random initial conditions.
- Any time a solution is desired for benchmark play (or real, competitive play) play each of the N candidate agents against all of the other N-1.
- Take the best player as the result of the overall process.
For instance, if we have each of the N=10 neural networks produced by the 10 optimizations above play the other N-1 = 9 networks 100 times and return +1 for a win, 0 for a draw, and -1 for a loss, then the average return for each network is
- 0.5162
- 0.5555
- 0.5485
- 0.5088
- 0.3668
- 0.5000
- 0.5500
- 0.5248
- 0.5035
- 0.4250
The NN from run #2 is selected as the best. Note that this final selection only uses self-play information.
Discussion¶
For the successful experiments above, OA used $nPlay=1$, a single simulation for each evaluation. One interpretation might be that using such a small value for $nPlay$ causes OA to play noisy moves that are biased toward better play. The noise helps the learner explore the game space, and the bias toward better play encourages steady improvement.
On the the other hand, you might wonder whether search is needed at all. Maybe just playing against the last best agent would be enough. Or maybe doing that and adding some noise might be enough to solve the problem. The list of negative results below suggest that these two ideas and many variations would not solve the problem.
The methods below rarely reached zero losses and were not stable: They did not stay at zero losses after continued optimization.
- Train against MC, increase # games in evaluation by 10% when # losses fell below 10 (minLoss=10)
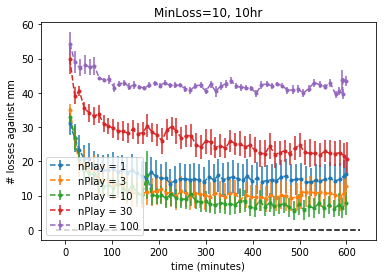
- Train against OA w/self embedded
The methods below did not achieve zero losses:
- Train against OA w/nPlay = 10
- Train against OA to maximize return over games [This differs from the successful method. The return is +1,-1,0 for win, lose, draw. Minimizing losses ignores the difference between winning and drawing.]
- Train against previous best w/exploration added by choosing a move randomly with probability $pRand$; tried $pRand = .1$ and $pRand = .5$
- Pure self-play
- Evaluate against previous best
- Evaluate against previous best w/various hall-of-fame ideas
Conclusion¶
We devised a novel adversary against which to train a neural-network based agent to play tic-tac-toe using an evolution strategy and self-play.
Evolution strategies seem well-matched to this sparse- and long-term-reward task. Additionally, they require little (none, in this case) hyperparameter tuning.
Self-play learning objectives have many pitfalls. They need to be constructed to encourage exploration of the game space and to discourage cycles of strategy dominance.